大家好，我是 Ai 学习的老章

测试几个大模型在 latex 公式识别中的表现

Kimi、Qwen-3-235B-A22B 是在网页中使用的，Claude-3.7-sonnet、GPT-4.1、Gemini 2.5 Pro 在 windsurf 中调用的。众所周知，DeepSeek 不是多模态，不参与此次对比，前端虽然支持图片输入，但其实是加了 OCR，并非 V3 or R1 的原生的视觉理解能力

省流版：

• 1、最强大的还是 Gemini 2.5 Pro
• 2、Claude-3.7-sonnet 和 GPT-4.1 没有出彩
• 3、Qwen-3-235B-A22B 还行，发挥很稳定，Qwen2 时就发现其水平可以
• 4、Kimi 出乎意料，都可以和 Qwen3 五五开了

第一题

中高难度，模糊手写，数字是欧洲写法，比如 7 中间加了一横，其中有一个 8 写的极像 6

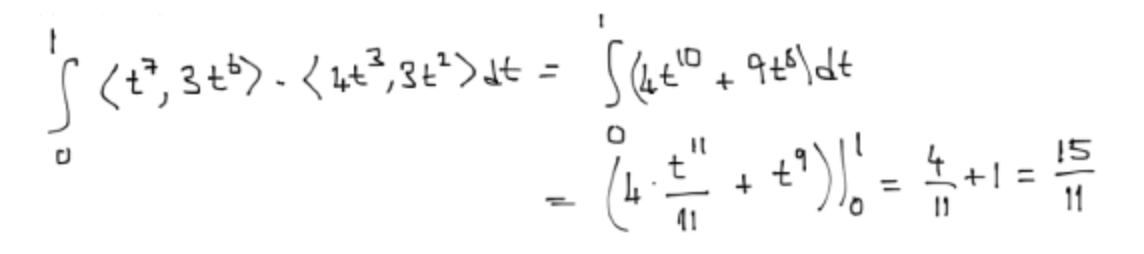
Kimi

$$\int_0^1 \langle t^7, 3t^b \rangle \cdot \langle 4t^3, 3t^2 \rangle dt = \int_0^1 (4t^{10} + 9t^6) dt = \left(4 \cdot \frac{t^{11}}{11} + t^9\right)\Bigg|_0^1 = \frac{4}{11} + 1 = \frac{15}{11}$$

Qwen-3-235B-A22B

$$\int_{0}^{1} \langle t^7, 3t^6 \rangle - \langle 4t^2, 3t^2 \rangle , dt = \int_{0}^{1} (4t^{10} + 9t^6) , dt = \left( 4 \cdot \frac{t^{11}}{11} + t^9 \right) \bigg|_{0}^{1} = \frac{4}{11} + 1 = \frac{15}{11}$$

Claude-3.7-sonnet

$$\int_0^1 \langle t^3, 3t^5 \rangle - \langle 4t^3, 3t^5 \rangle dt = \int_0^1 (4t^{10} + 9t^8) dt = \left( 4 \cdot \frac{t^{11}}{11} + t^9 \right) \bigg|_0^1 = \frac{4}{11} + 1 = \frac{15}{11}$$

GPT-4.1

$$ \int_0^1 \langle t^7,, 3t^5 \rangle \cdot \langle 4t^3,, 3t^2 \rangle , dt = \int_0^1 (4t^{10} + 9t^7) , dt = \left( 4 \cdot \frac{t^{11}}{11} + t^8 \right) \Bigg|_0^1 = \frac{4}{11} + 1 = \frac{15}{11} $$

Gemini 2.5 Pro

$$\int_0^1 \langle t^7, 3t^6 \rangle \cdot \langle 4t^3, 3t^2 \rangle dt = \int_0^1 (4t^{10} + 9t^8) dt = \left( 4 \frac{t^{11}}{11} + t^9 \right) \Big|_0^1 = \frac{4}{11} + 1 = \frac{15}{11}$$

结论：只有 Gemini 2.5 Pro 可以完成任务

第二题

简单点，印刷版

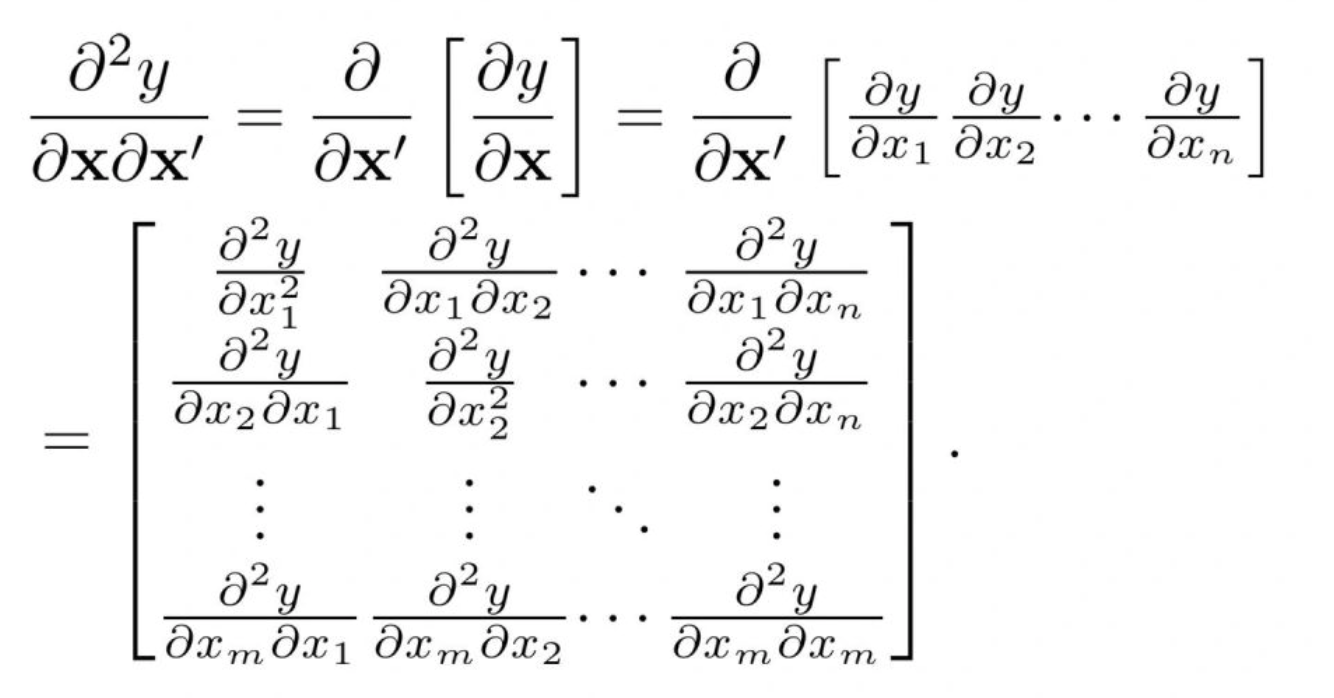
Kimi

$$\frac{\partial}{\partial \theta_j} J(\theta) = \frac{\partial}{\partial \theta_j} \frac{1}{2}(h_\theta(x) - y)^2 = 2 \cdot \frac{1}{2}(h_\theta(x) - y) \cdot \frac{\partial}{\partial \theta_j}(h_\theta(x) - y)$$

Qwen-3-235B-A22B

$$\frac{\partial}{\partial \theta_j} J(\theta) = \frac{\partial}{\partial \theta_j} \frac{1}{2} (h_\theta(x) - y)^2 = 2 \cdot \frac{1}{2} (h_\theta(x) - y) \cdot \frac{\partial}{\partial \theta_j} (h_\theta(x) - y)$$

Claude-3.7-sonnet

$$\frac{\partial}{\partial\theta_j}J(\theta) = \frac{\partial}{\partial\theta_j}\frac{1}{2}(h_\theta(x) - y)^2 = 2 \cdot \frac{1}{2}(h_\theta(x) - y) \cdot \frac{\partial}{\partial\theta_j}(h_\theta(x) - y)$$

GPT-4.1

$$ \frac{\partial}{\partial \theta_j} J(\theta) = \frac{\partial}{\partial \theta_j} \frac{1}{2} (h_\theta(x) - y)^2 \ = 2 \cdot \frac{1}{2} (h_\theta(x) - y) \cdot \frac{\partial}{\partial \theta_j} (h_\theta(x) - y) $$

Gemini 2.5 Pro

$$ \frac{\partial}{\partial \theta_j} J(\theta) = \frac{\partial}{\partial \theta_j} \frac{1}{2} (h_\theta(x) - y)^2 \ = 2 \cdot \frac{1}{2} (h_\theta(x) - y) \cdot \frac{\partial}{\partial \theta_j} (h_\theta(x) - y) $$

结论：都可以完成任务，这个太简单了

第三题

上难度，多个复杂公式一次识别

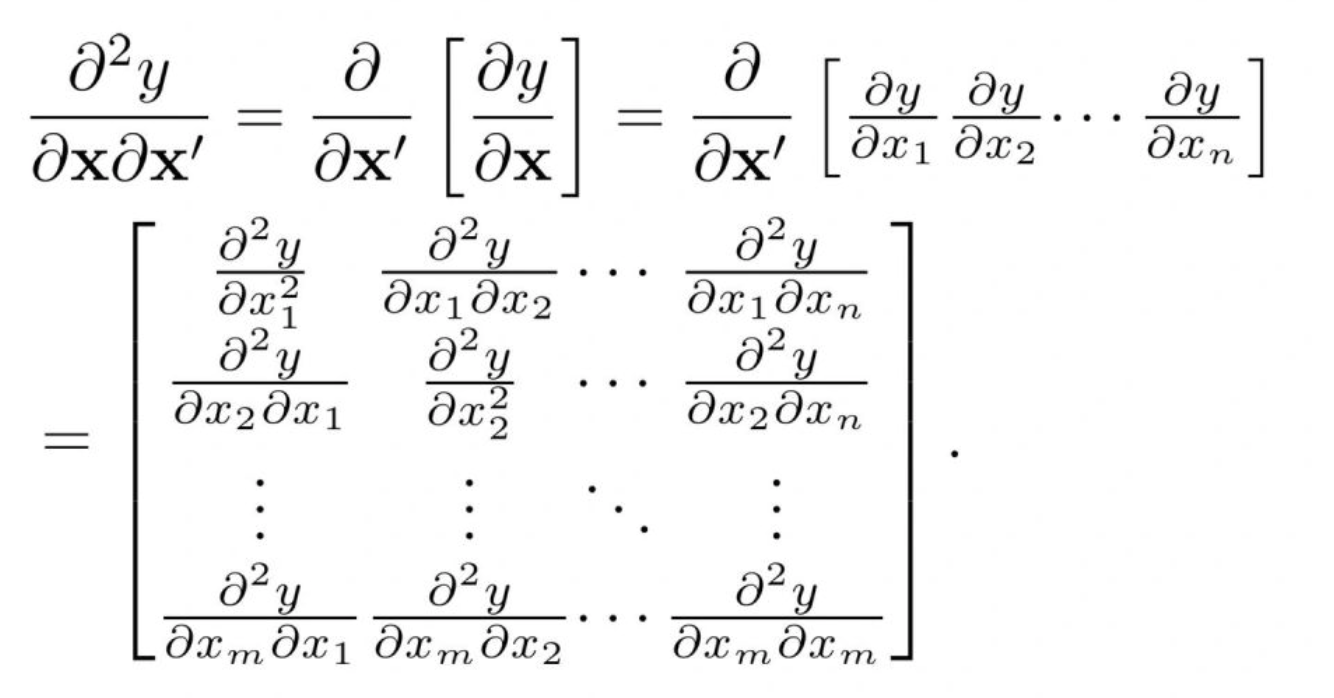
Kimi

$$\text{Gradient: } \nabla f = \left(\frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_1}\right) : \mathbb{R}^2 \rightarrow \mathbb{R}.$$ $$\text{Divergence: } \text{div}(v) = \frac{\partial v^1}{\partial x_1} + \frac{\partial v^2}{\partial x_2} : \mathbb{R}^2 \rightarrow \mathbb{R}.$$ $$\mathbb{L}^2(\mathbb{R}^2 \rightarrow \mathbb{R}) \xrightarrow{\quad \nabla \quad} \mathbb{L}^2(\mathbb{R}^2 \rightarrow \mathbb{R}^2) \xleftarrow{\quad \text{div} \quad}$$ $$\nabla f = (f_{k_1+1,k_2} - f_k, f_{k_1,k_2+1} - f_k)k$$ $$\text{div}(v) = v^1_k - v^1 + v^2_k - v^2_{k_1,k_2-1}$$ $$\mathbb{R}^{n \times n} \xrightarrow{\quad \nabla \quad} (\mathbb{R}^{n \times n})^2 \xleftarrow{\quad \text{div} \quad}$$

Qwen-3-235B-A22B

$$ \text{Gradient: } \nabla f = \left( \frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_1} \right): \mathbb{R}^2 \to \mathbb{R}. $$ $$ \text{Divergence: } \operatorname{div}(v) = \frac{\partial v^1}{\partial x_1} + \frac{\partial v^2}{\partial x_2}: \mathbb{R}^2 \to \mathbb{R}. $$ $$ \nabla f = (f_{k_1+1,k_2} - f_k, f_{k_1,k_2+1} - f_k)k $$ $$ \operatorname{div}(v) = v^1_k - v^1 + v^2_k - v^2_{k_1,k_2-1} $$ $$ \mathbb{R}^{n \times n} \xleftrightarrow{\substack{\nabla \ \text{div}}} (\mathbb{R}^{n \times n})^2 $$

Claude-3.7-sonnet

$$ \text{Gradient: } \nabla f = \left(\frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_1}\right) : \mathbb{R}^2 \rightarrow \mathbb{R}.

\text{Divergence: } \text{div}(v) = \frac{\partial v^1}{\partial x_1} + \frac{\partial v^2}{\partial x_2} : \mathbb{R}^2 \rightarrow \mathbb{R}.

\mathrm{L}^2(\mathbb{R}^2 \rightarrow \mathbb{R}) \xrightarrow{\nabla} \mathrm{L}^2(\mathbb{R}^2 \rightarrow \mathbb{R}^2) \ \mathrm{L}^2(\mathbb{R}^2 \rightarrow \mathbb{R}) \xleftarrow{\text{div}} \mathrm{L}^2(\mathbb{R}^2 \rightarrow \mathbb{R}^2)

\nabla f = (f_{k_1+1,k_2} - f_k, f_{k_1,k_2+1} - f_k)_k

\text{div}(v) = v^1_k - v^1_{k_1-1,k_2} + v^2_k - v^2_

\mathbb{R}^{n \times n} \xrightarrow{\nabla} (\mathbb{R}^{n \times n})^2 \ \mathbb{R}^{n \times n} \xleftarrow{\text{div}} (\mathbb{R}^{n \times n})^2 $$

GPT-4.1

$$ % 上半部分：连续情形 \textbf{Gradient:} \quad \nabla f = \left( \frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2} \right) : \mathbb{R}^2 \to \mathbb{R}.

\textbf{Divergence:} \quad \mathrm{div}(\mathbf{v}) = \frac{\partial v^1}{\partial x_1} + \frac{\partial v^2}{\partial x_2} : \mathbb{R}^2 \to \mathbb{R}.

L^2(\mathbb{R}^2 \to \mathbb{R}) \quad \xleftarrow{\quad \mathrm{div} \quad} \quad \boxed{\nabla \ \mathrm{div}} \quad \xrightarrow{\quad \nabla \quad} \quad L^2(\mathbb{R}^2 \to \mathbb{R}^2)

% 下半部分：离散情形 [ \nabla f = \left( f_{k_1+1,k_2} - f_k, ; f_{k_1,k_2+1} - f_k \right)_k ]

[ \mathrm{div}(\mathbf{v}) = v^1_k - v^1_{k_1-1,k_2} + v^2_k - v^2_{k_1,k_2-1} ]

\mathbb{R}^{n \times n} \quad \xleftarrow{\quad \mathrm{div} \quad} \quad \boxed{\nabla \ \mathrm{div}} \quad \xrightarrow{\quad \nabla \quad} \quad (\mathbb{R}^{n \times n})^2 $$

Gemini 2.5 Pro

$$ \text{Gradient: } \nabla f = \left( \frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_1} \right) : \mathbb{R}^2 \to \mathbb{R} \ \ \text{Divergence: } \text{div}(v) = \frac{\partial v^1}{\partial x_1} + \frac{\partial v^2}{\partial x_2} : \mathbb{R}^2 \to \mathbb{R} \ \ L^2(\mathbb{R}^2 \to \mathbb{R}) \mathrel{\overset{\nabla}{\underset{\text{div}}{\rightleftarrows}}} L^2(\mathbb{R}^2 \to \mathbb{R}^2) \ \ \nabla f = (f_{k_1+1, k_2} - f_k, f_{k_1, k_2+1} - f_k)k \ \ \text{div}(v) = v_k^1 - v^1 + v_k^2 - v_{k_1, k_2-1}^2 \ \ \mathbb{R}^{n \times n} \mathrel{\overset{\nabla}{\underset{\text{div}}{\rightleftarrows}}} (\mathbb{R}^{n \times n})^2 $$

结论：都还行，后面三个我在 windsurf 用的，不带自动渲染，换行有问题

第四题

底色非纯白，略复杂公式识别

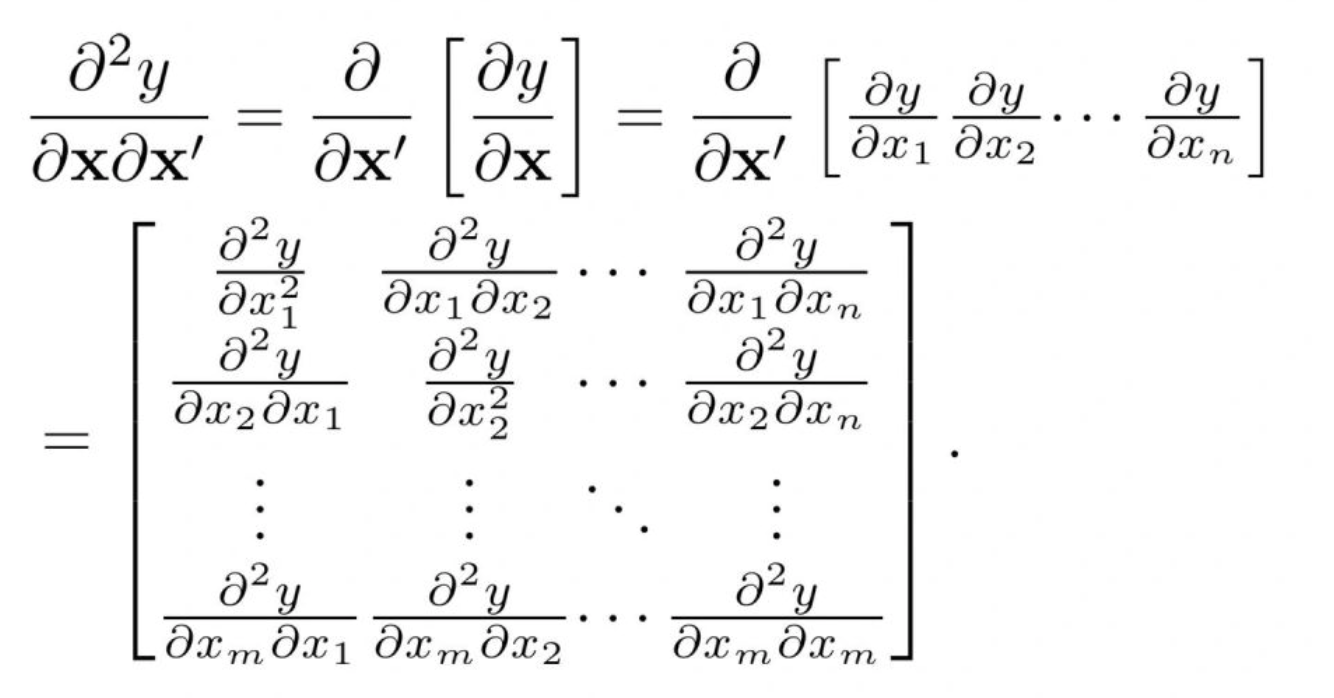
Kimi

$$[a_0, \ldots, a_n] \stackrel{\text{def.}}{=} a_0 + \frac{1}{a_1 + \frac{1}{a_2 + \frac{1}{a_3 + \ldots}}} \stackrel{\text{def.}}{=} a_0 + \frac{1}{[a_1, \ldots, a_n]} \stackrel{\text{def.}}{=} \frac{p_n}{q_n}$$

Qwen-3-235B-A22B

$$ [a_0, \ldots, a_n] \stackrel{\text{def.}}{=} a_0 + \cfrac{1}{a_1 + \cfrac{1}{a_2 + \cfrac{1}{a_3 + \cdots}}} \stackrel{\text{def.}}{=} a_0 + \frac{1}{[a_1, \ldots, a_n]} \stackrel{\text{def.}}{=} \frac{p_n}{q_n} $$

Claude-3.7-sonnet

$$[a_0, \ldots, a_n] \stackrel{\text{def.}}{=} a_0 + \frac{1}{a_1 + \frac{1}{a_2 + \frac{1}{a_3 + \ldots}}} \stackrel{\text{def.}}{=} a_0 + \frac{1}{[a_1, \ldots, a_n]} \stackrel{\text{def.}}{=} \frac{p_n}{q_n}$$

GPT-4.1

$$ \left[ a_0, \ldots, a_n \right] \overset{\text{def.}}{=} a_0 + \cfrac{1}{a_1 + \cfrac{1}{a_2 + \cfrac{1}{a_3 + \cdots}}} \overset{\text{def.}}{=} a_0 + \cfrac{1}{\left[ a_1, \ldots, a_n \right]} \overset{\text{def.}}{=} \frac{p_n}{q_n} $$

Gemini 2.5 Pro

$$ [a_0, \dots, a_n] \overset{\text{def.}}{=} a_0 + \frac{1}{a_1 + \frac{1}{a_2 + \frac{1}{a_3 + \dots}}} \overset{\text{def.}}{=} a_0 + \frac{1}{[a_1, \dots, a_n]} \overset{\text{def.}}{=} \frac{p_n}{q_n} $$ 结论：看样子难度页太低了，都 OK

第五题

复杂公式，带矩阵运算

Kimi

$$\frac{\partial^2 y}{\partial \mathbf{x} \partial \mathbf{x}'} = \frac{\partial}{\partial \mathbf{x}'} \left[ \frac{\partial y}{\partial \mathbf{x}} \right] = \frac{\partial}{\partial \mathbf{x}'} \left[ \frac{\partial y}{\partial x_1} \frac{\partial y}{\partial x_2} \ldots \frac{\partial y}{\partial x_n} \right]$$ $$= \begin{bmatrix} \frac{\partial^2 y}{\partial x_1^2} & \frac{\partial^2 y}{\partial x_1 \partial x_2} & \cdots & \frac{\partial^2 y}{\partial x_1 \partial x_n} \ \frac{\partial^2 y}{\partial x_2 \partial x_1} & \frac{\partial^2 y}{\partial x_2^2} & \cdots & \frac{\partial^2 y}{\partial x_2 \partial x_n} \ \vdots & \vdots & \ddots & \vdots \ \frac{\partial^2 y}{\partial x_m \partial x_1} & \frac{\partial^2 y}{\partial x_m \partial x_2} & \cdots & \frac{\partial^2 y}{\partial x_m \partial x_m} \end{bmatrix}.$$

Qwen-3-235B-A22B

$$ \frac{\partial^2 y}{\partial x \partial x'} = \frac{\partial}{\partial x'} \left[ \frac{\partial y}{\partial x} \right] = \frac{\partial}{\partial x'} \left[ \frac{\partial y}{\partial x_1} \frac{\partial y}{\partial x_2} \ldots \frac{\partial y}{\partial x_n} \right] $$ $$ = \begin{bmatrix} \frac{\partial^2 y}{\partial x_1^2} & \frac{\partial^2 y}{\partial x_1 \partial x_2} & \ldots & \frac{\partial^2 y}{\partial x_1 \partial x_n} \ \frac{\partial^2 y}{\partial x_2 \partial x_1} & \frac{\partial^2 y}{\partial x_2^2} & \ldots & \frac{\partial^2 y}{\partial x_2 \partial x_n} \ \vdots & \vdots & \ddots & \vdots \ \frac{\partial^2 y}{\partial x_m \partial x_1} & \frac{\partial^2 y}{\partial x_m \partial x_2} & \ldots & \frac{\partial^2 y}{\partial x_m \partial x_m} \end{bmatrix}. $$

Claude-3.7-sonnet

$$\frac{\partial^2 y}{\partial \mathbf{x} \partial \mathbf{x}'} = \frac{\partial}{\partial \mathbf{x}'}\left[\frac{\partial y}{\partial \mathbf{x}}\right] = \frac{\partial}{\partial \mathbf{x}'}\left[\frac{\partial y}{\partial x_1} \frac{\partial y}{\partial x_2} \cdots \frac{\partial y}{\partial x_n}\right] \ = \begin{bmatrix} \frac{\partial^2 y}{\partial x_1^2} & \frac{\partial^2 y}{\partial x_1 \partial x_2} & \cdots & \frac{\partial^2 y}{\partial x_1 \partial x_n} \ \frac{\partial^2 y}{\partial x_2 \partial x_1} & \frac{\partial^2 y}{\partial x_2^2} & \cdots & \frac{\partial^2 y}{\partial x_2 \partial x_n} \ \vdots & \vdots & \ddots & \vdots \ \frac{\partial^2 y}{\partial x_m \partial x_1} & \frac{\partial^2 y}{\partial x_m \partial x_2} & \cdots & \frac{\partial^2 y}{\partial x_m \partial x_m} \end{bmatrix}.$$

GPT-4.1

$$ \begin{align*} \frac{\partial^2 y}{\partial \mathbf{x} \partial \mathbf{x}'} &= \frac{\partial}{\partial \mathbf{x}'} \left[ \frac{\partial y}{\partial \mathbf{x}} \right] \ &= \frac{\partial}{\partial \mathbf{x}'} \left[ \frac{\partial y}{\partial x_1} \quad \frac{\partial y}{\partial x_2} \quad \cdots \quad \frac{\partial y}{\partial x_n} \right] \ &= \begin{bmatrix} \frac{\partial^2 y}{\partial x_1^2} & \frac{\partial^2 y}{\partial x_1 \partial x_2} & \cdots & \frac{\partial^2 y}{\partial x_1 \partial x_n} \ \frac{\partial^2 y}{\partial x_2 \partial x_1} & \frac{\partial^2 y}{\partial x_2^2} & \cdots & \frac{\partial^2 y}{\partial x_2 \partial x_n} \ \vdots & \vdots & \ddots & \vdots \ \frac{\partial^2 y}{\partial x_m \partial x_1} & \frac{\partial^2 y}{\partial x_m \partial x_2} & \cdots & \frac{\partial^2 y}{\partial x_m^2} \end{bmatrix} \end{align*} $$

Gemini 2.5 Pro

$$ \begin{align*} \frac{\partial^2 y}{\partial \mathbf{x} \partial \mathbf{x}'} &= \frac{\partial}{\partial \mathbf{x}'} \left[ \frac{\partial y}{\partial \mathbf{x}} \right] \ &= \frac{\partial}{\partial \mathbf{x}'} \left[ \frac{\partial y}{\partial x_1} \quad \frac{\partial y}{\partial x_2} \quad \cdots \quad \frac{\partial y}{\partial x_n} \right] \ &= \begin{bmatrix} \frac{\partial^2 y}{\partial x_1^2} & \frac{\partial^2 y}{\partial x_1 \partial x_2} & \cdots & \frac{\partial^2 y}{\partial x_1 \partial x_n} \ \frac{\partial^2 y}{\partial x_2 \partial x_1} & \frac{\partial^2 y}{\partial x_2^2} & \cdots & \frac{\partial^2 y}{\partial x_2 \partial x_n} \ \vdots & \vdots & \ddots & \vdots \ \frac{\partial^2 y}{\partial x_m \partial x_1} & \frac{\partial^2 y}{\partial x_m \partial x_2} & \cdots & \frac{\partial^2 y}{\partial x_m \partial x_n} \end{bmatrix}. \end{align*} $$ 结论：都可以

第六题

最高难度，模糊手写，公式混在文本中，横线与笔记本自带的线混在一起

Kimi

$$ \begin{align*} \frac{P(A_1(u,L,t) = a_1) \cdot P(A_2(v,L,t) = a_2)}{P(A_1(u,L,t) = a_1 \lor A_2(v,L,t) = a_2)} \end{align*} $$

Qwen-3-235B-A22B

$$ P(A_1(u, L, t) = a_1 \land A_2(v, L, t) = a_2 \mid \sigma_L(u) = v) $$

$$ P(A_1(u, L, t) = a_1) \cdot P(A_2(v, L, t) = a_2) $$

Claude-3.7-sonnet

$$ \begin{align} P(A_1(u,l,t) = a_1) \wedge P(A_2(v,l,t) = a_2) \mid \sigma_I(u) = v \ P(A_1(u,l,t) = a_1) \cdot P(A_2(v,l,t) = a_2) \ \sigma_I(u) = v \end{align} $$

GPT-4.1

$$ P\left(A_1(u, q, t) = a_1 \wedge A_2(v, q, t) = a_2 \mid I_u = I_v \right) $$

$$ P_{C,A}(u, q, t) = a_1,\quad P_{C,A}(v, q, t) = a_2 $$ $$

$$

Gemini 2.5 Pro

$$ \frac{P(A_1(u, l, t) = a_1 \land A_2(v, l, t) = a_2 | \sigma_t(u) = v)}{P(A_1(u, l, t) = a_1) \cdot P(A_2(v, l, t) = a_2)} $$

结论：只有 Gemini 2.5 Pro 成功

富哥们用 Gemini 2.5 Pro，我准备用 Qwen-3 了

制作不易，如果这篇文章觉得对你有用，可否点个关注。给我个三连击：点赞、转发和在看。若可以再给我加个🌟，谢谢你看我的文章，我们下篇再见！

搭建完美的写作环境：工具篇（12 章）图解机器学习 - 中文版（72 张 PNG）ChatGPT、大模型系列研究报告（50 个 PDF）108 页 PDF 小册子：搭建机器学习开发环境及 Python 基础  116 页 PDF 小册子：机器学习中的概率论、统计学、线性代数  史上最全！371 张速查表，涵盖 AI、ChatGPT、Python、R、深度学习、机器学习等